XVI Spin
The electron also has an intrinsic angular momentum , independently of its orbital angular momentum . This intrinsic angular momentum is called spin (the name suggests that the electron performs a rotation around itself, which is, however, actually not the case).
XVI.1 Stern-Gerlach experiment
The spin was discovered in the Stern-Gerlach experiment in 1922. In this experiment, silver atoms are heated in an oven, from which they escape through a tiny hole. They travel into direction and enter an apparatus where they pass through an inhomogeneous magnetic field . This field points into direction and has a finite gradient . If the atoms carry a magnetic moment this gives rise to a force
| (279) |
which deflects the atoms into direction.

In the experiment it is observed that the atoms arrive on the screen at two spots, only. This is not what is classically expected, but also incompatible with quantisation of the orbital angular momentum , which always yields an odd number of possible values of since is an integer. However, the experiment can be fully explained by introducing an intrinsic magnetic moment
| (280) |
where has the properties of angular momentum, but with not an integer. Since the spin magnetic quantum number is restricted to this allows only two values , hence
| (281) |
Given the force from Eq. (279) it can be deduced that the observed locations of the arriving atoms indeed correspond to these two values.
XVI.2 Spinor
The spin state of the electron is described by a two-component vector (called spinor)
| (282) |
where
| (283) | |||||
| (284) |
Hence describes an electron with spin up and describes an electron with spin down.
The scalar product of spinors is given by (see the mathematical appendix)
| (285) |
Normalisation of the probability requires , hence .
XVI.3 Spin operators
The spin operator consists of the three spin matrices
| (286) | |||
| (287) | |||
| (288) |
The three matrices
| (289) |
are called Pauli matrices.
XVI.4 Eigenvalues and eigenvectors of and
Since
| (293) |
all vectors are eigenvectors . The eigenvalue corresponds to angular momentum with , see Eq. (266).
Since
| (294) |
the normalised eigenvectors of are (with eigenvalue ) and (with eigenvalue ). This again corresponds to angular momentum with , see Eq. (267).
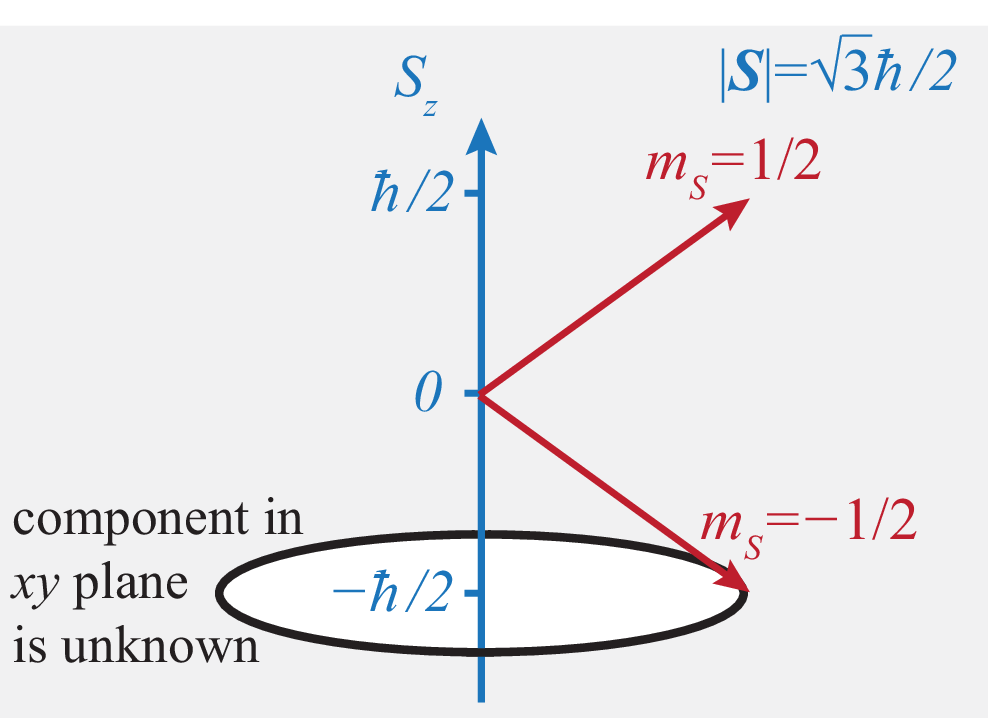
XVI.5 Eigenvalues and eigenvectors of and
| (295) |
Hence the normalised eigenvectors of are (with eigenvalue ) and (with eigenvalue ).
| (296) |
Hence the normalised eigenvectors of are (with eigenvalue ) and (with eigenvalue ).
XVI.6 Expectation values
The expectation value of is given by
| (297) | |||||
Note that
| (298) | |||||
| (299) |
are the probabilities for spin up and down, respectively.
By similar calculations,
| (300) | |||||
| (301) |
where Re denotes the real part and Im denotes the imaginary part of the complex number .
The probabilities for spin measurements in or directions are given by
| (302) | |||||
| (303) |
and
| (304) | |||||
| (305) |
respectively.
XVI.7 Polarisation vector and Bloch sphere
A convenient alternative way to represent a spinor state is given by the 3-dimensional real polarisation vector
| (306) | |||||
| (307) |
If is normalised then the polarisation vector is of unit length, i.e., it is restricted to the surface of a sphere, the so-called Bloch sphere.
XVI.8 Stationary Schrödinger equation
The most general stationary Hamiltonian for a spin is a hermitian -dimensional matrix. Such a matrix can always be written as
| (308) |
where , , , and are real constants, and
| (309) |
is the -dimensional identity matrix. The stationary Schrödinger equation is solved by the eigenvectors of . These can be found by writing the vector , where is a unit vector and . The eigenvectors can then be written as
| (310) | |||||
| (311) |
On the Bloch sphere, these eigenvectors correspond to the polarisation vectors
| (312) |
The corresponding eigenvalues
| (313) |
determine the energy of these states.
XVI.9 Spin in Dirac notation
In order to describe spin in the Dirac notation, we introduce the normalised and mutually orthogonal states for “spin up” and for “spin down”, with
| (314) |
Accordingly, we can write
| (315) |
The other spin components are then given by the operators
| (316) |
and the total spin is given as
| (317) |
The eigenstates of are , while those of are ; the associated eigenvalues are . All the expressions for expectation values and probabilities given above can now be seen as special incarnations of our general rules for quantum mechanics, evaluated in the basis , .
In analogy to orbital angular momentum, we can also introduce the ladder operators
| (318) |
which are again non-hermitian and related by . These now convert or annihilate spin eigenstates, according to
| (319) |
XVI.10 Mathematical appendix: two-dimensional linear algebra
XVI.10.1 Vectors and matrices
A vector in two dimensions is given by two numbers and , called components,
| (320) |
Matrices , etc are given by four numbers, such as
| (321) |
| (322) |
We consider the case that the matrix and vector components can be complex numbers.
XVI.10.2 Addition of vectors and matrices
Vectors and matrices are added element by element,
| (323) |
| (324) |
XVI.10.3 Scalar product
The scalar product
| (325) |
can also be written as the product
| (326) |
where denotes the hermitian conjugate.
A vector is said to be normalised when .
XVI.10.4 Multiplication of a vector and a matrix
When a vector is multiplied by a matrix , the result is a new vector with components
| (327) |
One can also multiply two matrices and , which results in another matrix
| (328) |
Note that this is different from element-by-element multiplication.
XVI.10.5 Eigenvalues and eigenvectors
Given is a matrix . The eigenvalue equation
| (329) |
requires to find vectors such that the matrix multiplication only changes the length of the vector (multiplication by the constant ), but not its direction. The number is called eigenvalue. In general, the eigenvalues are found from the equation , where is the determinant, . This gives the two solutions
| (330) |
The corresponding eigenvectors can be written as
| (331) |
XVI.10.6 Revision Quiz
For
calculate
(i) ,
(ii) ,
(iii) ,
(iv) ,
(v) ,
(vi) ,
(vii) the eigenvalues and eigenvectors of .